The complex Ginzburg-Landau equation

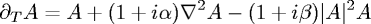
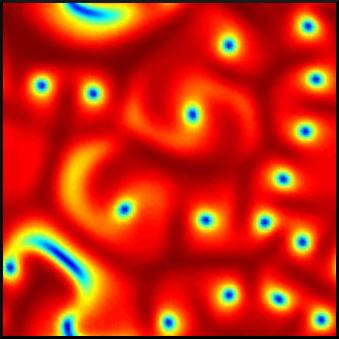
is one of the most-studied equations in applied mathematics. It describes qualitatively, and often quantitatively, a vast array of phenomena including nonlinear waves, second-order phase transitions, Rayleigh-Bénard convection and superconductivity. The equation describes the evolution of amplitudes of unstable modes for any process exhibiting a Hopf bifurcation, for which a continuous spectrum of unstable wavenumbers is taken into account. It can be viewed as a highly general normal form for a large class of bifurcations and nonlinear wave phenomena in spatially extended systems.

In this tutorial, a broad overview of the behaviour of the equation is given, with a focus on the one-dimensional case. The linear stability problem of plane wave solutions to the equation is expounded and the analysis is complemented with a graphical representation of the various observed behaviours. Two MATLAB programs are also provided, which simulate the 1D and 2D versions of the complex Ginzburg-Landau equation, allowing the reader to verify the results presented here and to conduct their own exploration of the equation.